Question

verify that parallelogram abcd with vertices a(-5 -1) b(-9,6) c(-1,5) d(3,-2) is a rhombus by showing that it is a parallelogram with perpendicular diagonals

Answer 1

Answer: Showed.

Step-by-step explanation: Given vertices of parallelogram abcd are a(-5,-1), b(-9,6), c(-1,5) and d(3,-2).

Since it is a parallelogram, so opposite sides must be equal. That is,

ab = cd, bc = ad.

We are to show abcd is a rhombus by showing that the diagonals ac and bd are perpendicular to each other.

Now,

`ab=√((-5+9)^2+(-1-6)^2)=√(16+49)=√(65),\\\\bc= √((-9+1)^2+(6-5)^2)=√(64+1)=√(65).`

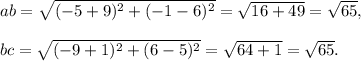
So, ab = bc = cd = da, with proves that all the sides are equal.

Now, slope of diagonal ac will be

`S_(ac)=(5+1)/(-1+5)=(3)/(2),`

and the slope of bd will be

`S_(bd)=(-2-6)/(3+9)=-(2)/(3).`

Therefore,

`S_(ac)* S_(bd)=-1.`

This shows that the diagonals ac and bd are perpendicular.

Thus, the parallelogram abcd is a rhombus.