Question

A person on a runway sees a plane approaching. The angle of elevation from the runway to the plane is 11.1° . The altitude of the plane is 4000 fr. What is the horizontal distance from the plane to the person on the runway.

Answer 1

The horizontal distance from the plane to the person on the runway is 20408.16 ft.

Explanation:

Consider the figure below,

Where AB represent altitude of the plane is 4000 ft above the ground , C represents the runner. The angle of elevation from the runway to the plane is 11.1°

BC is the horizontal distance from the plane to the person on the runway.

We have to find distance BC,

Using trigonometric ratio,

`\tan\theta=(Perpendicular)/(base)`

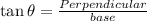
Here,
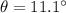`\theta=11.1^(\circ)` ,Perpendicular AB = 4000

`\tan\theta=(AB)/(BC)`

`\tan 11.1^(\circ) =(4000)/(BC)`

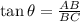
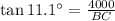
Solving for BC, we get,

`BC=(4000)/(\tan 11.1^(\circ) )`

`BC=(4000)/(0.196)` (approx)

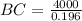`BC=20408.16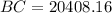`(approx)

Thus, the horizontal distance from the plane to the person on the runway is 20408.16 ft