Question

1/2x+1/3y=9 and 3/5x-3/4y=-3
use elimination method​

Answer 1

(10, 12 )

Explanation:

let's begin by clearing the fractions from both equations

`(1)/(2)` x +
`(1)/(3)` y = 9 ( multiply through by 6 ( the LCM of 2 and 3 to clear ) )

3x + 2y = 54 → (1)

`(3)/(5)` x -
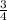`(3)/(4)` y = - 3 ( multiply through by 20 ( the LCM of 5 and 4 to clear ) )

12x - 15y = - 60 → (2)

multiplying (1) by - 4 and adding to (2) will eliminate x )

- 12x - 8y = - 216 → (3)

add (2) and (3) term by term to eliminate x

0 - 23y = - 276

- 23y = - 276 ( divide both sides by - 23 )

y = 12

substitute y - 12 into either of the 2 equations and solve for x

substituting into (1)

3x + 2(12) = 54

3x + 24 = 54 ( subtract 24 from both sides )

3x = 30 ( divide both sides by 3 )

x = 10

solution is (10, 12 )

Answer 2

(You could do this shorter, but by the time i realized that it was too late.)

First, we need one of the variables (x or y) to have the same coefficient.
Lets use the variable y, since it uses smaller numbers.

Multiply the first equation by the denominator of y, which is 3. Then multiply the second equation by the denominator of y in the second equation, which is 4.

You get:
1st equation:
`(3)/(2) x+ y = 27`
2nd equation:
`(12)/(5)x - 3y=-12`
Now we need to multiply the first equation by 3, so we can have "3y" in both of the equations.
1st equation: 9/2x + 3y = 81
2nd equation:
`(12)/(5)x - 3y=-12`
Now we can subtract both of the equations.
12/5x + 9/2x = 69 We need to make the common denominator for x.
24/10x + 45/10x = 69
69/10x=69
x=10
Now we substitute x into the first equation (or the second, doesn't matter).
1/2 * 10 + 1/3y=9
5 + 1/3y = 9
1/3 y = 4
y = 12