Answer:
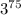
Step-by-step explanation:
We are asked to divide our given fraction:
 .
.
We will simplify our division problem using rules of exponents.
Using product rule of exponents
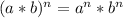 we can write:
we can write:
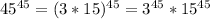
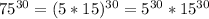
Substituting these values in our division problem we will get,
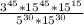
Using power rule of exponents
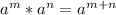 we will get,
we will get,
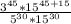
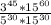
Using quotient rule of exponent
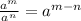 we will get,
we will get,

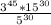
Using product rule of exponents
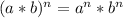 we will get,
we will get,
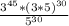
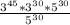
Upon canceling out
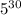 we will get,
we will get,

Using power rule of exponents
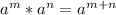 we will get,
we will get,
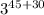
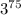
Therefore, our resulting quotient will be
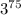 .
.