Question

How do i do this???????????????????????????????????

Answer 1

The y-intercept is (0, -6).

Explanation:

The question is asking you to find the equation of the line that passes through the point (7, 1) and is parallel to line j, which means that the line has the same slope as line j.

To find the slope of line j, you would use the slope formula:
`(y_2-y_1)/(x_2-x_1)`.

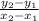• Use the points on line j: (4, 1), (-3, -6). Substitute in -6 for
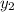  `y_2` and 1 for
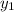  `y_1`. Substitute -3 for
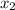  `x_2` and 4 for
  `x_1`.
• 
  `((-6)-(1))/((-3)-(4)) \rightarrow (-7)/(-7) = 1`
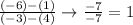
• The slope of line j is 1, therefore the equation of the line we are writing will also have a slope of 1 since they must be parallel.

To write the equation of the line, use the point-slope formula because we are given the two things in the name of the formula---a point that the line passes through (7, 1) and the slope of the line (1).

• Point-slope form is
  `y-y_1=m(x-x_1)`
• Substitute 1 for
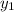  `y_1`, 1 for m, and 7 for
  `x_1`.
• 
  `y-(1)=1(x-(7))`
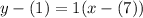
• Simplify: y - 1 = 1(x - 7)
• Distribute 1 inside the parentheses.
• y - 1 = x - 7
• Add 1 to both sides of the equation.
• y = x - 6

The question wants you to find the y-intercept of the equation. To find the y-intercept, make x = 0.

• y = (0) - 6
• Subtract 0 - 6.
• y = -6

A point is shown as (x, y). We made x = 0 and found that y = -6, so if you substitute these values into (x, y) the y-intercept will be (0, -6).