Question

Place the steps for finding f(x) in the correct order.

H
11
K
f(1) = 41 + 7
0·0-0-0-0

Answer 1

For finding the inverse of a function you have to write it as an ecuation.

`y = 4x + 7`

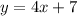
Invert the values of x and y.

`x = 4y + 7`

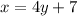
Our objetive now in this new equation is to clear y. First, subtract 7 in both sides of the equation.

`x - 7 = 4y`

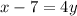
Then, divide both sides by 4.

`(x - 7)/(4) = y`

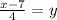
Finally, invert the values of x and y again and put the equation like a function.

`{f}^( - 1) (x) = (x - 7)/(4)`

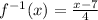
This is correct because f(x) = x is the axis of symmetry for both functions (green one).

Answer 2

0
The answer is C
Ik this bc
Someone told me