Answer:
We use log to solve only those equations in which we have our variables in power form.
Explanation:
Given : Margee thinks she can use logs to solve
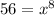 , since logs seem to make exponents disappear but Margee is wrong
, since logs seem to make exponents disappear but Margee is wrong
We have to explain the difference between equations like
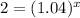 and
and
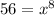
We use log to solve only those equations in which we have our variables in power form.
Out of given equation only
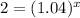 has x in power form so we can apply log for solving the equation as,
has x in power form so we can apply log for solving the equation as,
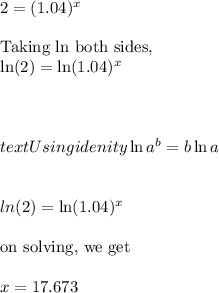
While solving other equation ,
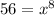 , we can directly take 8 root both side,
, we can directly take 8 root both side,
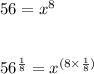
Thus, We use log to solve only those equations in which we have our variables in power form.