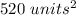1 Answer

Shivani Katukota · Answer 1 · 2020-02-06T15:07:48+0000

For this case, we have that the area of the surface of the figure shown is given by:

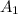A_(1) : The area of the upper rectangle (inclined)

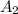A_(2) : The area of the two triangles.

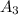A_(3) : The area of the base of the prism

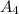$A_ {4}$ : The area of the rear rectangle

We apply Pythagoras to know the length of the inclined side of the rectangle:

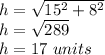
$h = \sqrt {15 ^ 2 + 8 ^ 2}\\h = \sqrt {289}\\h = 17 \ units$

Thus, the
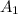A_(1) is given by:

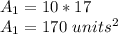
$A_ {1} = 10 * 17\\A_ {1} = 170 \ units ^ 2$

We look for the area given by the triangles, knowing that the area of a triangle is
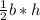$\frac {1} {2} b * h$ , then:

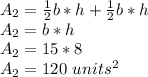
$A_ {2} = \frac {1} {2} b * h + \frac {1} {2} b * h\\A_ {2} = b * h\\A _(2) = 15 * 8\\A_(2) = 120 \ units ^ 2$

We look for the area of the base of the prism:

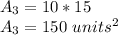
$A_ {3} = 10 * 15\\A_ {3} = 150 \ units ^ 2$

We look for the area of the posterior rectangle:

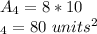
$A_ {4} = 8 * 10\\\A_ {4} = 80 \ units ^ 2$

Adding we have:

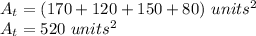
$A_ {t} = (170 + 120 + 150 + 80) \ units ^ 2\\A_ {t} = 520 \ units ^ 2$

Answer:

$520 \ units ^ 2$

Please log in or register to add a comment.