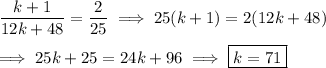Question

Problem

(a) Let
`a_1, a_2, a_3,...` be an arithmetic progression of non-zero numbers with common difference
`d`.
(i) Show that
`(1)/(a_na_(n+1))=(1)/(da_n)-(1)/(da_(n+1))` for any
`n\geq1`.
(ii) Hence show that
`(1)/(a_1a_2)+(1)/(a_2a_3)+(1)/(a_3a_4)+...+(1)/(a_(99)a_(100))=(99)/(a_1a_(100))`.
(b) For what value of
`k` does
`(1)/(3*7)+(1)/(7*11)+(1)/(11*15)+...+(1)/(k(k+4))+(2)/(25)`?

Answer 1

(a.i) If
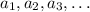`a_1,a_2,a_3,\ldots` are in arithmetic progression, then there is a constant
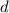`d` such that

`a_(n+1) - a_n = d`

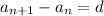
for all
`n\ge1`. In other words, the difference
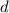`d` between any two consecutive terms in the sequence is always the same.

`a_2-a_1 = a_3-a_2 = a_4-a_3 = \cdots = d`

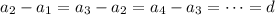
Now, we can expand the target expression into partial fractions.

`\frac1{a_na_(n+1)} = (\alpha)/(a_n) + (\beta)/(a_(n+1))`

Combining the fractions on the right and using the recursive equation above, we have

`\frac1{a_na_(n+1)} = (\alpha (a_n + d) + \beta a_n)/(a_n(a_n+d)) = ((\alpha+\beta) a_n + \alpha d)/(a_n a_(n+d)) \\\\ \implies \begin{cases}\alpha + \beta = 0 \\ \alpha d = 1 \end{cases} \implies \alpha = \frac1d, \beta = -\frac1d`

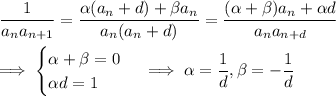
and hence

`\frac1{a_n a_(n+1)} = \frac1{da_n} - \frac1{da_(n+1)}`

as required.

(a.ii) Using the previous result, the
`n`-th term
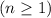`(n\ge1)` in the sum on the left is

`\frac1{a_n a_(n+1)} = \frac1d \left(\frac1{a_n} - \frac1{a_(n+1)}\right)`

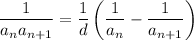
Expand each term in this way to reveal a telescoping sum:

`\frac1{a_1a_2} + \frac1{a_2a_3} + \frac1{a_3a_4} + \cdots + \frac1{a_(99)a_(100)} \\\\ ~~~~~~~~ = \frac1d \left(\left(\frac1{a_1} - \frac1{a_2}\right) + \left(\frac1{a_2} - \frac1{a_3}\right) + \left(\frac1{a_3} - \frac1{a_4}\right) + \cdots + \left(\frac1{a_(99)} - \frac1{a_(100)}\right)\right) \\\\ ~~~~~~~~ = \frac1d \left(\frac1{a_1} - \frac1{a_(100)}\right) = (a_(100) - a_1)/(d a_1 a_(100))`

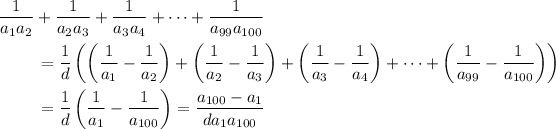
By substitution, we can show

`a_n = a_(n-1) + d = a_(n-2) + 2d = \cdots = a_1 + (n-1)d \\\\ \implies a_(100) = a_1 + 99d`

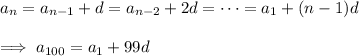
so that the last expression reduces to

`((a_1 + 99d) - a_1)/(d a_1 a_(100)) = (99d)/(d a_1 a_(100)) = (99)/(a_1 a_(100))`

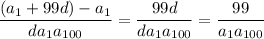
as required. More generally, it's easy to see that

`\frac1{a_1a_2} + \frac1{a_2a_3} + \frac1{a_3a_4} + \cdots + \frac1{a_na_(n+1)} = (n)/(a_1a_(n+1))`

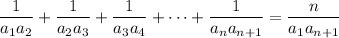
(b) I assume you mean the equation

`\frac1{3*7} + \frac1{7*11} + \frac1{11*15} + \cdots + \frac1{k(k+4)} = \frac2{25}`

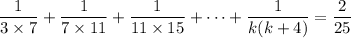
Note that the distinct factors of each denominator on the left form an arithmetic sequence.

`a_1 = 3`

`a_2 = 3 + 4 = 7`

`a_3 = 7 + 4 = 11`

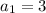
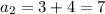
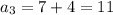
and so on, with
`n`-th term

`a_n = 3 + (n-1)*4 = 4n - 1`

Let
`a_n=k`. Using the previous general result, the left side reduces to

`\frac1{3*7} + \frac1{7*11} + \frac1{11*15} + \cdots + \frac1{a_na_(n+1)} = \frac n{3a_(n+1)} \\\\ \implies \frac{\frac{k+1}4}{3(k+4)} = \frac2{25}`

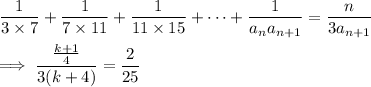
Solve for
`k`.

`(k+1)/(12k+48) = \frac2{25} \implies 25(k+1) = 2(12k+48) \\\\ \implies 25k + 25 = 24k + 96 \implies \boxed{k=71}`