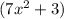Answer:
Width:
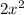
Lenght:
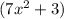
Explanation:
1. The prime factorization of the monomial is:

2. The product of the common factors is:
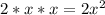
3. The greatest common monomial factor is:
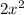
4. The formula for calculate the area of a rectangle is:
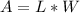
Where L is the length and W is the width
5. Therefore, if the greatest common monomial factor monomial of the area of
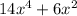 is
is
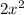 and the area is the product of the lenght and the width, you have that the lenght is:
and the area is the product of the lenght and the width, you have that the lenght is:
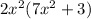
Length: