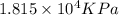Question

Trimix 10/50 is a gas mixture that contians 10% oxygen and 50% helium, and the rest is nitrogen. If a tank of trimix 10/50 has a total pressure of 2.07 x 104 kPa, then what is the partial pressure of helium?

Answer 1

Answer: I believe it would be 2.07 x 10^3 kPa

Step-by-step explanation:

Answer 2

Answer : The partial pressure of helium is,
`1.815* 10^4KPa`

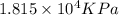
Solution : Given,

Molar mass of
`O_2` = 32 g/mole

Molar mass of helium = 4 g/mole

Molar mass of
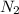`N_2` = 28 g/mole

Total pressure of gas =
`2.07* 10^4KPa`

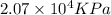
As we are given gases in percent, that means 10 g of oxygen gas, 50 g of helium gas and 40 g of nitrogen gas present in 100 g of mixture.

First we have to calculate the moles of oxygen, helium and nitrogen gas.

`\text{Moles of }O_2=\frac{\text{Mass of }O_2}{\text{Molar mass of }O_2}=(10g)/(32g/mole)=0.3125moles`

`\text{Moles of }He=\frac{\text{Mass of }He}{\text{Molar mass of }He}=(50g)/(4g/mole)=12.5moles`

`\text{Moles of }N_2=\frac{\text{Mass of }N_2}{\text{Molar mass of }N_2}=(40g)/(28g/mole)=1.428moles`

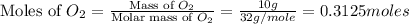
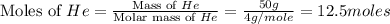
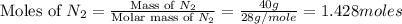
Now we have to calculate the total number of moles of gas mixture.

`\text{Total number of moles of gas}=\text{Moles of oxygen gas}+\text{Mole of helium gas}+\text{Moles of nitrogen gas}`

`\text{Total number of moles of gas}=0.3125+12.5+1.428=14.24moles`

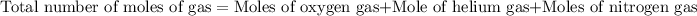
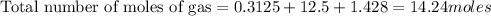
Now we have to calculate the moles fraction of helium gas.

`\text{Mole fraction of He gas}=\frac{\text{Moles of He gas}}{\text{Total number of moles of gas}}=(12.5)/(14.25)=0.877`

Now we have to calculate the partial pressure of helium.

`p_(He)=X_(He)* P_T`

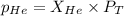
where,

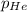`p_(He)` = partial pressure of helium

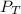`P_T` = total pressure

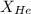`X_(He)` = mole fraction of helium

Now put all the given values in this formula, we get

`p_(He)=(0.877)* (2.07* 10^4KPa)=1.815* 10^4KPa`

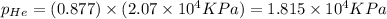
Therefore, the partial pressure of helium is,
`1.815* 10^4KPa`