Question

Suppose that a cyclist began a 306 mile ride across a state in the eastern edge of the state, at the same time that a car traveling toward it leaves the western end of the state. If the bicycle and car met after 4.5 hr and the car traveled 31.6 mph faster than the bicycle, find the average rate of each.

Answer 1

Answer: The average rate of bicycle and car are 18.2 mph and 49.8 mph respectively.

Explanation:

Since we have given that

Distance covered = 306 miles

Time taken by bicycle and car met = 4.5 hours

Let the speed of the bicycle be 'x mph'

Let the speed of the car be 'x+31.6 mph'.

Since they are moving in opposite directions.

So, their relative speed will be

`x+x+31.6\\\\=2x+31.6\ mph`

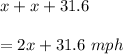
As we know the formula for "Distance-speed":

`Speed=(Distance)/(Time)\\\\2x+31.6=(306)/(4.5)\\\\2x+31.6=68\\\\2x=68-31.6\\\\2x=36.4\\\\x=(36.4)/(2)=18.2\ mph`

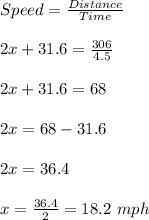
So, The speed of bicycle is 18.2 mph

and the speed of car is given by

`18.2+31.6\\\\=49.8\ mph`

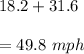
Hence, the average rate of bicycle and car are 18.2 mph and 49.8 mph respectively.