Question

In the diagram below, MNPQ is a parallelogram whose diagonals are perpendicular. Prove: MNPQ is a rhombus.

Answer 1

Given : MNPQ is a parallelogram whose diagonals are perpendicular.

To prove : MNPQ is a rhombus.

Proof:

In parallelogram MNPQ,

R is the intersection point of the diagonals MP and NQ( shown in below diagram)

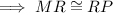`\implies MR\cong RP` (Because, the diagonals of parallelogram bisects each other)

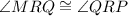`\angle MRQ\cong \angle QRP` (Right angles )

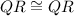`QR\cong QR` (Reflexive)

Thus, By SAS postulate of congruence,

`\triangle MRQ\cong \triangle PRQ`

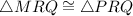
By CPCTC,

`MQ\cong QP`

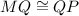
Similarly,

We can prove,
`\triangle MRN\cong \triangle PRN`

By CPCTC,

`MN\cong NP`

But, By the definition of parallelogram,

`MN\cong QP` and
`MQ\cong NP`

⇒
`MN\cong NP\cong PQ\cong MQ`

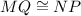
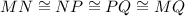
All four side of parallelogram MNQP are congruent.

⇒ Parallelogram MNPQ is a rhombus.

Hence, proved.