Answer:
The value of function
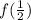 is
is

Explanation:
Given : function
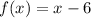
We have to find the value of function at
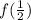
Consider the given function
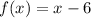
We have to find the value of function at
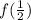
that is at
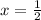
Put x =
 in function , we have,
in function , we have,
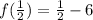
Taking LCM , we have
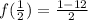
Solving , we have
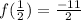
Thus, the value of function
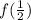 is
is
