Question

what is the sum of the measures of the interior angles of a regular polygon if each exterior angle measures 72°

Answer 1

108°

Explanation:

Answer 2

The sum of the measures of the interior angles of a regular polygon if each exterior angle measures 72° is 540°.

Explanation:

The formula to find the measure of each exterior angle of a regular polygon is

`Exterior=(360)/(n)`

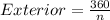
It is given that the measure of each exterior angle of a regular polygon is 72°.

`72=(360)/(n)`

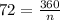
Multiply both sides by n.

`72n=360`

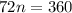
Divide both sides by 72.

`n=(360)/(72)`

`n=5`

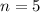
It means the number of vertices of the polygon is 5. It means the given polygon is pentagon.

The sum of interior angles of a regular polygon is

`Sum=(n-2)* 180`

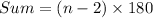
Substitute n=5.

`Sum=(5-2)* 180`

`Sum=3* 180`

`Sum=540`

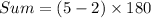
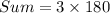
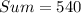
Therefore the sum of the measures of the interior angles of a regular polygon if each exterior angle measures 72° is 540°.