Answer:
The correct option is 3.
Explanation:
If a line passing through two points, then the equation of line is
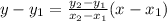
Rel line passing through the points (0,-2) and (2,0), then related equation of red line is

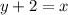
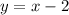
Since the shaded region is above the line and the related line is a solid line therefore the sign of inequality must be ≥. The first inequality is
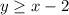
Blue line passing through the points (0,2) and (4,0), then related equation of red line is

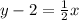
Multiply 2 on both the sides.
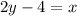
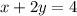
(0,0) is in the shaded region. So, the inequity must be satisfy by (0,0).


The related line is dotted, so the required sign of inequality is <. The second inequality is
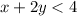
The system of linear inequalities is defined as
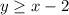
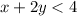
Therefore the correct option is 3.