Question

DRAW A RAY TO COMPLETE AOB WITH A MEASURE OF 35?

Answer 1

1. Correct answer:

straight

Since the points A, O and B lies on the same line, the form a straight line. Therefore, the measure of the angle ∠AOB = 180°. In this way, 180° angles are called straight angles. We can write this segment in terms of two points. For instance, we can name this segment as
`\overline{AB} \ or \ \overline{BA}`

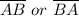
2. Correct answer:

Acute

If two lines, rays or line segments meet, they form an angle. So the measure of an angle is how much you need to rotate one of the lines so it lies on the top of the other. Since we need to have a measure of 35°, that is, ∠AOB = 35°. From this notation, the first point is A, the vertex is O and the other point is B, then we must draw a ray from the point O and make an angle with a measure of 35° as indicated in the first figure below. This is an acute angle because if an angle has a measure less than 90°, it's called an acute angle

3. Correct answer:

Obtuse

Since we need to have a measure of 103°, that is, ∠COD = 103°, from this notation, the first point is C, the vertex is O and the other point is D, then we must draw a ray from the point O and make an angle with a measure of 103° as indicated in the second figure below. This is an obtuse angle because if an angle has a measure greater than 90°, but also less than 180°, it's called an obtuse angle.

4. Correct answer:

145°

The measure of the angle ∠BOC = 145°. This angle can be found from different ways. First, by taking a look on the protractor, we can realize that his measure is 145°. Second, as we know from the previous questions that ∠AOB = 35° and ∠AOC = 180°, hence we can say that:

∠BOC = ∠AOC - ∠AOB

∴ ∠BOC = 180° - 35° = 145°

5. Correct answer:

77°

The measure of the angle ∠AOD = 77°. As in the previous exercise, this angle can be found from different ways. First, by taking a look on the protractor, we can realize that his measure is 77°. Second, as we know from 3. that ∠COD = 103° and ∠AOC = 180°, hence we can say that:

∠AOD = ∠AOC - ∠COD

∴ ∠AOD = 180° - 103° = 77°

This is an acute angle.

6. Correct answer:

42°

This angle can be found in different ways. First of all, this angle is:

∠BOD = ∠AOD - ∠AOB

∴ ∠BOD = 77° - 35° = 42°

Another way we can use to find this is:

∠BOD = 180° - ∠AOB - ∠COD

∴ ∠BOD = 180° - 35° - 103° = 42°

The representation of this problem has been attached in the third figure below. This is an acute angle.

Answer 2

Answer: Acute (First option).

Explanation:

1. You know that the angle ∠AOB must be 35°.

2. Then, you must place the midpoint of the protactor on the poinr O, which is the vertex of the angle.

3. As the side of the angle AO is lined up with the zero of the set of number that goes from 0 to 180, you must draw the ray between that set. Keeping this on mind, you obtain the angle ∠AOB shown in the figure attached.

4. By definition, when the measure of an angle is between 0° and 90° is called "Acute". Therefore, the angle ∠AOB is acute.