Answer:
The other sides of triangles are 8.72 in and 8.72 in
Explanation:
In a triangle ABC. Please find the attachment for figure.
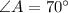
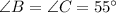
Side BC=a = 10 in
Using sine law of trigonometry,
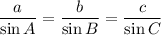
Substitute the given value into formula.
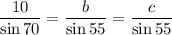
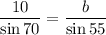
Cross multiply and we get
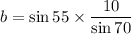
 in
in
It is a isosceles triangle. Therefore, b=c=8.72 in
Hence, The other sides of triangles are 8.72 in and 8.72 in