Question

Which point does not lie on the circle centered at A(3, 1) and passing through the origin (0, 0)? A. J(2, -2) B. K(6, 0) C. L(4, -4) D. M(2, 4)

Answer 1

The correct answer is C

Explanation:

The given circle is centered at A(3, 1) and passes through the origin (0, 0).

The radius of this circle can be found using the distance formula;

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`.

`\Rightarrow r=√((3-0)^2+(1-0)^2)`.

`\Rightarrow r=√((3)^2+(1)^2)`.

`\Rightarrow r=√(9+1)`.

`\Rightarrow r=√(10)`.

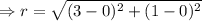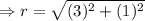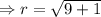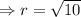The equation of this circle is given by

`(x-a)^2+(y-b)^2=r^2`

Where
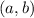`(a,b)` is the centre.

We substitute the center and radius to obtain;

`(x-3)^2+(y-1)^2=(√(10))^2`

`(x-3)^2+(y-1)^2=10`

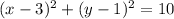
Option A

When we substitute (2,-2) into this equation we get;

`(2-3)^2+(-2-1)^2=10`

`1+9=10`

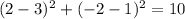
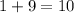
This is true

Option B

When we substitute K(6,0), we get,

`(6-3)^2+(0-1)^2=10`

`9+1=10`

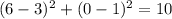
This is also true

Option C

We substitute L(4,-4) to get;

`(4-3)^2+(-4-1)^2=10`

`1+25=10`

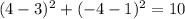
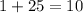
This is false. Hence L(4,-4) does not lie on the circle.

Option D

We substitute M(2,4)

`(2-3)^2+(4-1)^2=10`

`1+9=10`

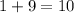
This is also true.

The correct answer is C