Question

If A = (2,4) and B = (7, 3) find the magnitude and direction of the vector AB.

Answer 1

QUESTION 1

Given A = (2,4) and B = (7, 3),


`^( \rightarrow ) _(AB) = \binom{7}{3} - \binom{2}{4}`


`^( \rightarrow ) _(AB) = \binom{5}{ - 1}`

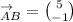
The magnitude of the vector is


`|^( \rightarrow ) _(AB) | = \sqrt{ {5}^(2) + {( - 1)}^(2) }`


`|^( \rightarrow ) _(AB) | = √( 25+ 1)`


`|^( \rightarrow ) _(AB) | = √( 26) \: units`

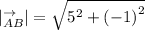
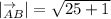
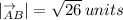
QUESTION 2

The vector is


`^( \rightarrow ) _(AB) = \binom{5}{ - 1}`

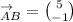
The y component is negative. This means the vector is in the 4th quadrant.

In bearing we measure the direction from the north pole in the clockwise direction.

The direction of the vector is


`(90+\theta) \degree`

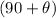
Where


`\tan( \theta) = (1)/(5)`


`\theta ={tan}^( - 1)( (1)/(5))`


`\theta =11.31`

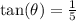
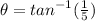
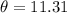
The direction is


`(90+11.31) \degree`


`=101.31\degree`


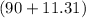
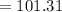
`=101\degree` to the nearest degree.