Question

Which values of x would make a polynomial equal to zero if the factors of the polynomial were (x+3) and (x+12)

Answer 1

A product of factors is zero if and only if one or more of the factors is zero. That is, if ab = 0, then either a = 0 or b = 0 (or both).

Hence (x+3)(x+12) = 0 only if (x+3) = 0 or (x+12) = 0 or both. (x+3) = 0 when x = 3.(x+12) = 0 when x = 12.

Hence the values of x that make (x+3)(x+12) = 0 are x = 3 and x = 12.

Answer 2

The value of x is -3 and -12 which make a polynomial equal to zero.

Explanation:

Given : The factors of the polynomial were (x+3) and (x+12).

To find : Which values of x would make a polynomial equal to zero.

Solution :

The factors of the polynomial were (x+3) and (x+12).

To find the value of x we equation the product of factors equate to zero.

i.e.
`(x+3)(x+12)=0`

`(x+3)=0\text{ (or) }(x+12)=0`

`x=-3\text{ (or) }x=-12`

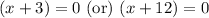
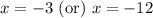
So, The value of x is -3 and -12 which make a polynomial equal to zero.