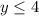QUESTION 1
The given function is
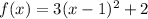
This function is of the form:
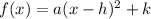 , where
, where
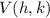 is the vertex of the function.
is the vertex of the function.
Hence the vertex is
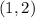
The function is defined for all real values of
 . Hence the domain is all real numbers.
. Hence the domain is all real numbers.
To find the range, we let
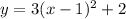
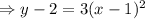
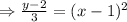
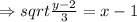

 is defined for
is defined for
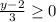
 is defined for y\geq 2[/tex]
is defined for y\geq 2[/tex]
The correct answer is A
QUESTION 2
Based on the description, I was able to picture the diagram as shown in the attachment.
This graph has the vertex
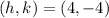 , Hence the equation is of the form:
, Hence the equation is of the form:
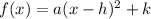
The equation is
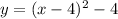
The correct answer is A
QUESTION 3
Based on the description, the graph has vertices (2,1)
Since this is a minimum graph;
The equation is of the form;
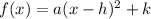 , where
, where
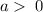 .
.
Hence the equation is

The correct answer is A.
QUESTION 5
The given function is
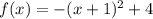
This equation is of the form
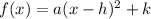 where
where
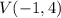 is the vertex .
is the vertex .
The function is defined for all real values of
 . Hence the domain is all real numbers.
. Hence the domain is all real numbers.
To find the range, we let
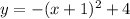
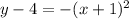
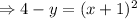
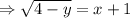
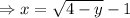
 is defined for
is defined for
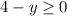
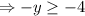
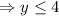
Hence the range is the range is
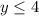
B) The vertex is (–1, 4), the domain is all real numbers, and the range is