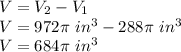Question

Caleb has two basketballs. The brown basketball has a radius of 6 inches. The orange basketball has a radius of 9 inches. How much more air does the orange basketball hold than the brown basketball? A 36? in.3 B 76? in.3 C 684? in.3 D 1216? in.3

Answer 1

Answer: Option C.

Explanation:

1. To solve this problem you must apply the formula for calculate the volume of a sphere, which is shown below:

`V=(4)/(3)r^(3)\pi`

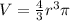
Where r is the radius of the sphere.

2. The volume of the brown basketball is:

`V_1=(4)/(3)(6in)^(3)\pi=288\pi`
`in^(3)`

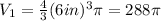
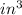
3. The volume of the orange basketball is:

`V_2=(4)/(3)(9in)^(3)\pi=972\pi`
`in^(3)`

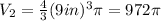
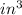
4. Then to calculate how much more air the orange basketball holds than the brown basketball, you must subtract the volumes. So, the result is:

`V=V_2-V_1\\V=972\pi \ in^(3)-288\pi \ in^(3)\\V=684\pi\ in^(3)`