
★ Radius of first sphere
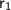 = 6cm.
= 6cm.
★ Radius of second sphere
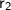 = 8cm.
= 8cm.
★ Radius of third sphere
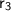 = 10cm.
= 10cm.

★ The radius of the resulting sphere formed.
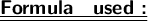
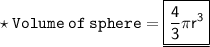

★ As, three spheres are melted to from one new sphere. Therefore, volume of three old sphere is equal to volume of new sphere.
i.e, Volume of first sphere + volume of second sphere + volume of third sphere = Volume of new sphere.

Let,
The radius of resulting sphere be
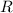
According to the question,
• Volume of first sphere + volume of second sphere + volume of third sphere = Volume of new sphere.
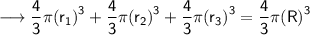
• here
☆
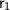 = 6cm
= 6cm
☆
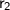 = 8cm
= 8cm
☆
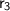 = 10cm
= 10cm
Putting the values,
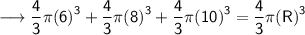
Taking "
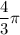 " common,
" common,
![\longrightarrow \sf (4)/(3) \pi \bigg[ {(6)}^(3) + {(8)}^(3) + {(10)}^(3) \bigg] = (4)/(3) \pi {(R)}^(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/b3bovt32d0hc17nthyidy8jiny3wzk6wms.png)
![\longrightarrow \sf \cancel{ (4)/(3) \pi} \bigg[ {(6)}^(3) + {(8)}^(3) + {(10)}^(3) \bigg] = \cancel{ (4)/(3) \pi } {(R)}^(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/imcr0fn77ub8xhweed7w4pux9vsx1gau6p.png)
![\longrightarrow \sf \bigg[ {(6)}^(3) + {(8)}^(3) + {(10)}^(3) \bigg] = {(R)}^(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/b4n3dmid9ipi0prpugjuqgg9z1vxiocjy4.png)
![\longrightarrow \sf \bigg[ 216 +512 + 1000 \bigg] = {(R)}^(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/e1ivssw73knvh9gk93y4nuq2quucasjck1.png)
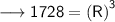
![\longrightarrow \sf \sqrt[3]{1728} = R](https://img.qammunity.org/2023/formulas/mathematics/high-school/rax6xoq1oro5m85v2udaxgotlgx090khlm.png)
![\longrightarrow \sf \sqrt[3]{ 12 * 12 * 12 } = R](https://img.qammunity.org/2023/formulas/mathematics/high-school/fzudc81omxs0iyijjgklvxhan6pvpmkf18.png)
![\longrightarrow \sf \sqrt[3]{ {(12)}^(3) } = R](https://img.qammunity.org/2023/formulas/mathematics/high-school/3crodm5y7p4zl4pevymm8e3sfdl6i5obyl.png)
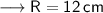
Therefore,
Radius of the resulting sphere is 12cm.

★ Figure in attachment.
