Question

What is the degree of (f*g)(x)?

Answer 1

Degree of fog(x) is 6

Explanation:

Degree of the function is highest exponent of the variable .

In order to find that we shall find the composition of the function as follows :

fog(x) is given by f(g(x))

And here f(x) =
`3x^2`

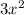
f(g(x)) will be
`3(g(x))^2`

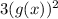
and then plugging the value of g(x) =
`4x^3+1`

so fog(x) = f(g(x)) =
`3(4x^3+1)^2`

=
`3(4x^3+1)^2=3(16x^6+1+8x^3)\\`

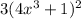
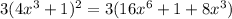
Here highest exponent of the function is 6

therefore degree of ( fog)(x) is 6.

Answer 2

Answer: 6

Explanation:

Degree of a function is the highest power of the variable present in a monomial.

Here, The given functions are,

`f(x) = 3x^2`

And,
`g(x) = 4x^3+1`

Thus,
`(fog)(x) = f[g(x)] = f[4x^3+1] = 3(4x^3+1)^2 = 3(16x^6+1+8x^3)`

Since, In the function fog the highest power of x is 6.

⇒ The degree of (fog)(x) is 6.