Question

When x increases from a to a + 2, y increases by a factor of 1 4 . For which functions is this statement true? A) y = 3(2)x B) y = 2x + 5 C) y = 7(0.5)x D) y = 1 2 x - 4

Answer 1

Option: C is correct.

`y=7* (0.5)^x`

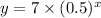
Explanation:

We are given that when x increases from 'a' to 'a+2' then y must increase by a factor of 1/4=0.25.

i.e. when x=a and x'=a+2.

then
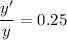`(y')/(y)=0.25` where y' is the function after putting x' to the old function.

A)

`y=3* 2^x`

when x=a

`y=3* 2^a`

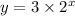
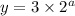
when x'=a+2

`y'=3* 2^(a+2)\\\\y'=3* 2^a* 2^2\\\\y'=3* 2^a* 4\\\\y'=4* y\\\\(y')/(y)=4\\eq (1)/(4)`

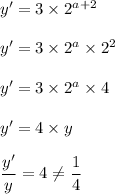
Hence, option (A) is incorrect.

B)

`y=2x+5`

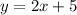
when x=a

`y=2a+5`

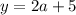
when x'=a+2

`y'=2(a+2)+5\\\\y'=2a+4+5\\\\\\y'=y+4`

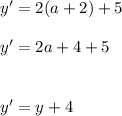
Here we do not get a factor of
`(1)/(4)`.

Hence, option B is incorrect.

C)

`y=7* (0.5)^x`

when x=a

`y=7* (0.5)^a`

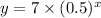
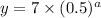
when x'=a+2

`y=7* (0.5)^(a+2)\\\\y=7* (0.5)^a* (0.5)^2\\\\y=y* 0.25\\\\(y')/(y)=0.25`

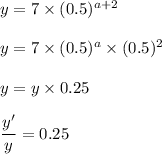
Hence we get a factor of
`(1)/(4)=0.25`

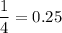
Hence, option C is correct.

D)

`y=(1)/(2)x-4`

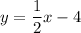
when x=a

`y=(1)/(2)a-4`

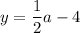
when x'=a+2

`y'=(1)/(2)(a+2)-4\\\\y'=(1)/(2)a+1-4\\\\y'=y+1`

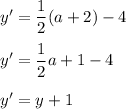
Here also we did not get a factor of
`(1)/(4)`.

Hence, option D is incorrect.

Hence, the function is:

`y=7* (0.5)^x`

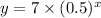
Hence, option C is correct.