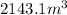Question

A cone-shaped pile of gravel has a diameter of 30 m and a height of 9.1 m.

Which estimate best approximates the volume of the pile of gravel?

Answer 1

2140 m^3 approximately.

Explanation:

The volume of a cone is 1/3 π r^2 h

Here r = 15 and h = 9.1

so the vulume is about 1/3 * 3.14 * 15^2 * 9.1

= 2140 m^3 approximately.

Answer 2

Volume(V) of the cone is given by:

`V = (1)/(3) \pi r^2h`

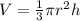
where,

r is the radius of the cone and h is the height of the cone.

As per the statement:

A cone-shaped pile of gravel has a diameter of 30 m and a height of 9.1 m.

⇒diameter(d) = 30 m and h = 9.1 m

Diameter(d) is given by:

`d = 2r`

then;

`30 = 2r`

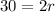
Divide both sides by 2 we have;

15 = r

or

r = 15 m

Substitute the given values and use
`\pi = 3.14` we have;

`V = (1)/(3) \cdot 3.14 \cdot 15^2 \cdot 9.1`

`V = (1)/(3) \cdot 3.14 \cdot 225 \cdot 9.1`

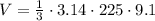
Simplify:

V = 2143.05 cubic meter.

Therefore, the best approximate the volume of the pile of gravel is,
`2143.1 m^3`