Answer:
Option (b) is correct.
The temperature of the metal after two hours is 28 Celsius
Explanation:
Given : A heated piece of metal cools according to the function
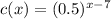 , where x is measured in hours and then a cooling device id added that aids in cooling according to the function
, where x is measured in hours and then a cooling device id added that aids in cooling according to the function
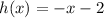
We have to determine the temperature of the metal after two hours.
Let w(x) denotes the temperature of metal .
Thus, w(x) can be given by function c(x) + h (x) = [c + h](x)
Thus,
\\\\w(x)=(0.5)^(x-7)+(-x-2)\\\\](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nziimfguetk8cponsccekuikmob0pr2u4v.png) , where x is measured in hours.
, where x is measured in hours.
Thus, after two hours that is when x = 2
the temperature of metal is given by w(2)

Solving , we get,
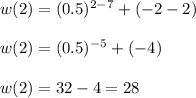
Thus, the temperature of the metal after two hours is 28 Celsius.
Hence, Option (b) is correct.