Question

If I initially have a gas at a pressure of 12 atm, volume of 23 liters, and temperature of 200 K, and then I raise the pressure to 14 atm and increase the temperature to 300 K, what is the new volume of the gas?

Answer 1

Hello!

If I initially have a gas at a pressure of 12 atm, volume of 23 liters, and temperature of 200 K, and then I raise the pressure to 14 atm and increase the temperature to 300 K, what is the new volume of the gas?

We have the following data:

P1 (initial pressure) = 12 atm

V1 (initial volume) = 23 L

T1 (initial temperature) = 200 K

P2 (final pressure) = 14 atm

T2 (final temperature) = 300 K

V2 (final volume) = ? (in L)

Now, we apply the data of the variables above to the General Equation of Gases, let's see:

`(P_1*V_1)/(T_1) =(P_2*V_2)/(T_2)`

`(12*23)/(200) =(14*V_2)/(300)`

`(276)/(200) =(14\:V_2)/(300)`

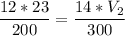
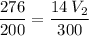
multiply the means by the extremes

`200*14\:V_2 = 276*300`

`2800\:V_2 = 82800`

`V_2 = \frac{82800\!\!\!\!\!\!\!\frac{\hspace{0.4cm}}{~}}{2800\!\!\!\!\!\!\!\frac{\hspace{0.4cm}}{~}}`

`V_2 \approx 29.57142857... \to \boxed{\boxed{V_2 \approx 30\:L}}\:\:\:\:\:\:\bf\blue{\checkmark}`

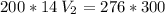
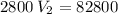
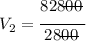
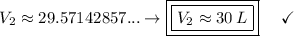
*** Note: the approximation rule says that when the number before the digit 5 ​​is odd, the previous value is raised to the next even number

Answer:

The new volume is approximately 30 Liters

_______________________

`\bf\green{I\:Hope\:this\:helps,\:greetings ...\:Dexteright02!}\:\:\ddot{\smile}`

Answer 2

Answer : The volume of gas will be 29.6 L

Step-by-step explanation:

Combined gas law is the combination of Boyle's law, Charles's law and Gay-Lussac's law.

The combined gas equation is,

`(P_1V_1)/(T_1)=(P_2V_2)/(T_2)`

where,

`P_1` = initial pressure of gas = 12 atm

`P_2` = final pressure of gas = 14 atm

`V_1` = initial volume of gas = 23 L

`V_2` = final volume of gas = ?

`T_1` = initial temperature of gas = 200K

`T_2` = final temperature of gas = 300K

Now put all the given values in the above equation, we get the final pressure of gas.

`(12atm* 23L)/(200K)=(14* V_2)/(300K)`

`V_2=29.6L`

Therefore, the new volume of gas will be 29.6 L