Answer:
Explanation:
It is given that A pyramid has a rectangular base with edges of length 10 and 24. The vertex of the pyramid is directly 13 units above the center of the base.. then The total surface area = area of rectangular base + area of 2 isosceles triangles with a base of 24 units + area of 2 isosceles triangles with a base of 10 units.
Area of rectangular base =
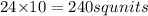
The slant height of isosceles triangles with a base of 24 units =
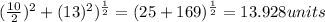 .
.
The area of 2 isosceles triangles with a base of 24 units=
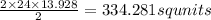
The slant height of isosceles triangles with a base of 10 units =
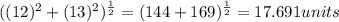
The area of 2 isosceles triangles with a base of 10 units=
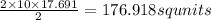
The total surface area of the pyramid = 240 + 334.281 + 176.918 = 591.97 sq units.