Question

I need answers asap... please

Proove the following trigonometric identities
...please no intentional wrong answers

Answer 1

see explanation

Explanation:

(4)

consider the left side

factor the numerator

cosx - cos³x = cosx(1 - cos²x)

`(cosx(1-cos^2x))/(sinx)[/tex = [tex](cosxsin^2x)/(sinx)`

cancel sinx on numerator/denominator

= cosxsinx =right side ⇒ verified

(5)

Consider the left side

expand the factors

(1 + cotΘ)² + (1 - cotΘ)²

= 1 + 2cotΘ + cot²Θ + 1 - 2cotΘ + cot²Θ

= 2 + 2cot²Θ

= 2(1 + cot²Θ) ← 1 + cot²Θ = cosec²Θ

= 2cosec²Θ = right side ⇒ verified

(6)

Consider the left side

the denominator simplifies to

cosxtanx = cosx ×
`(sinx)/(cosx)` = sinx

`(sin^2x(secx+cosecx))/(sinx)`

= sinx(
`(1)/(cosx)` +
`(1)/(sinx)`)

=
`(sinx)/(cosx)` +
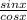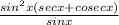
`(sinx)/(sinx)`

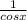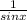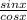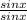
= tanx + 1 = right side ⇒ verified