For what values of x is the expression below defined? radical x plus 4 divided by radical 1 minus x

Question

asked Apr 15, 2020 167k views

2 Answers

Jespertheend · Answer 1 · 2020-04-20T13:47:52+0000

Answer: The function is defined in the interval [-4,0)

Explanation:

Here the given expression is,

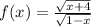
f(x)=(√(x+4) )/(√(1-x) )

⇒
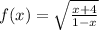
$f(x)=\sqrt{(x+4)/(1-x)$

Since, the function can not be defined if the value inside the square root is negative,

Thus, we can write,

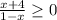
$(x+4 )/(1-x) \geq 0$

⇒
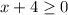
$x+4 \geq 0$

⇒
$x\geq -4$

Also,
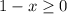
$1-x \geq 0$

But, if the denominator is zero the function can not be defined.

Thus,
1 - x > 0

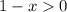
⇒ 1 > x

Thus, For the function f(x), -4 ≤ x <1

Hence, the Domain of the given function is [-4,0)