Answer:
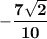
Explanation:
It is given that θ is between 270° and 360°, which means that θ is located in Quadrant IV ⇒ (x > 0, y < 0). Furthermore, the half-angle will be between 135° and 180°, which means the half-angle is in Quadrant II ⇒
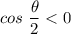
It is given that sin θ =
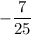 ⇒ y = -7 & hyp = 25
⇒ y = -7 & hyp = 25
Use Pythagorean Theorem to find "x":
x² + y² = hyp²
x² + (-7)² = 25²
x² + 49 = 625
x² = 576
x = 24
Use the "x" and "hyp" values to find cos θ:

Lastly, input cos θ into the half angle formula:
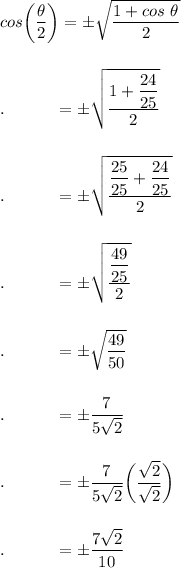
Reminder: We previously determined that the half-angle will be negative.