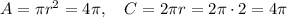The area of a circle is given by
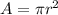
whereas the circumference is given by

If we want these two values to be (numerically) the same we have to set
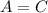 and solve for the radius:
and solve for the radius:
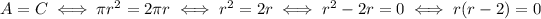
So, one (trivial) solution is
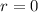 . A circle with radius 0 is just a point, and so both area and circumference are zero.
. A circle with radius 0 is just a point, and so both area and circumference are zero.
The other solution is
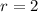 . In fact, you have
. In fact, you have