Answer: The answer is f(x) = - 2x²+12x-22.
Step-by-step explanation: We are given to write the function describing a parabola with vertex (3, -4) and passing through the point (5, -12).
We know that the standard form of a parabola with vertex (h, k) is given by
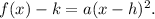
Here (h, k) = (3, -4), so we have
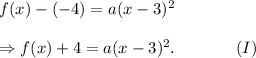
Also, the parabola is passing through the point (5, -12), so
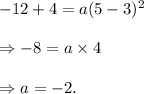
Substituting the value of 'a' above in equation (I), we have
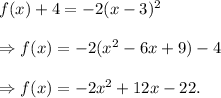
Thus, the answer is f(x) = - 2x²+12x-22..