Question

What is the probability that the number of “HEADs” on these four coins is equal to 3? (4 points)

a. 1/4
b. 1/16
c. 1/8
d. 1/36
e. None of these

Answer 1

a.
`(1)/(4)`

Step-by-step explanation:

We are asked to find the probability of getting 3 heads on 4 flips.

`\text{Probability}=\frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}`

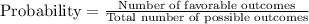
Since we know that flipping a fair coin has 2 equally likely possible outcomes, so flipping four coins will have
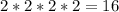`2*2*2*2=16` possible outcomes.

Sample space of possible outcomes.

HHHH, HHHT, HHTH, HHTT, HTHH, HTHT, HTTH, HTTT,

THHH, THHT, THTH,THTT, TTHH, TTHT, TTTH, TTTT.

We can see that there are 4 favorable outcomes of getting heads.

`\text{Probability of getting 3 heads}=(4)/(16)`

`\text{Probability of getting 3 heads}=(1)/(4)`

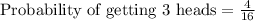
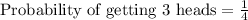
Therefore, the probability of getting 3 heads on 4 coins will be
`(1)/(4)` and option a is the correct choice.