Question

Which of the following statements are true about graphs of polynomial functions? Check all that apply. The local maximum and local minimum always occur at a turning point. The local maximum is the x-value of the coordinate at that point. The ends of an even-degree polynomial either both approach positive infinity or both approach negative infinity.

Answer 1

Answer:1 and 3

Explanation:

Answer 2

Answer: The answers are

(i) The local maximum and local minimum always occur at a turning point.

(iii) The ends of an even-degree polynomial either both approach positive infinity or both approach negative infinity.

Step-by-step explanation: We are given three statements and we are to check which of these are true about the graphs of polynomial functions.

In the attached figure (A), the graph of the polynomial function
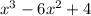`x^3-6x^2+4` is drawn. We can see that the local maximum occurs at the turning point P and local minimum occurs at the turning point Q. Also, the local maximum is not equal to the x-value of the coordinate at that point

Thus, the first statement is true. and second statement is false.

Again, in the attached figure (B), the graph of the even degree polynomial
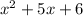`x^2+5x+6` is drawn. We can see that both the ends approaches to positive infinity and in case of
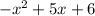`-x^2+5x+6`, both the ends approch to negative infinity.

Thus, the third statement is true.

Hence, the correct statements are first and third.