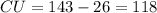Question

PLEASE HELP ME!! I DONT UNDERSTAND!!

Answer 1

`\large\boxed{CU=118}`

Explanation:

ΔUFW and ΔCDW are similar (AA). Therefore the siades are in proportion:

`(UW)/(CW)=(VW)/(DW)`

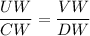
We have

UW = 36x-1

CW = 26

VW = 110

DW = 20

Substitute:

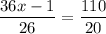`(36x-1)/(26)=(110)/(20)` cross multiply

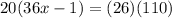`20(36x-1)=(26)(110)` use distributive property

`(20)(36x)+(20)(-1)=2860`

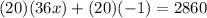
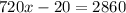`720x-20=2860` add 20 to both sides

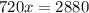`720x=2880` divide both sides by 720

`x=4`

`UW=36x-1\to UW=36(4)-1=144-1=143`

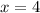
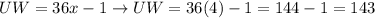
CU = UW - CW

Susbtitute:

`CU=143-26=118`