Question

In f(x) = 2x2 − 8x − 10, the y-intercept is ? at ? and the x-intercepts are (-1, 0) and ? .

Answer 1

1. y-intercept

`\boxed{(0,-10)}`

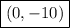
The quadratic function
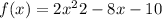`f(x)=2x^22-8x-10` represents a parabola. In fact, the graph of a quadratic function is a special type of U-shaped curve called a parabola. To find the y intercept, we set
`x=0` as follows:

`f(x)=2x^2-8x-10 \\ \\ If \ x=0 \rightarrow f(0)=-10 \\ \\ Then \ y-intercept: \\ \\ (0,-10)`

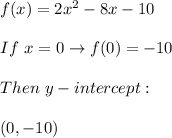
2. x-intercepts

`\boxed{(-1,0) \ and \ (5,0)}`

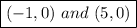
To find the other x-intercept, we must set
`y=0` as follows:

`f(x)=2x^2-8x-10 \\ \\ If \ y=0 \rightarrow 2x^2-8x-10=0 \\ \\ Using \ the \ quadratic \ formula: \\ \\ x=(-b \pm √(b^2-4ac))/(2a) \\ \\ \therefore x=(-(-8) \pm √((-b)^2-4(2)(-10)))/(2(2)) \\ \\ \therefore x_(1)=-1 \ and \ x_(2)=5`

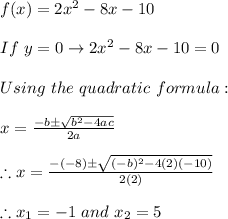
Therefore, the other x-intercept is
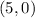`(5,0)`. You can see both the y-intercept and the x-intercepts in the figure below.