Answer: - 25.8 kJ
The overall process of interest in the question is the following
Hg (g) (650 K) → Hg (l) (297 K)
However, for mercury to pass from a gaseous state in 650 K to a liquid state in 297 K, it must go through a series of steps:
Step 1. Gaseous mercury at 650 K should cool down to 629.88 K, temperature corresponding to the vaporization temperature of this substance.
Step 2. Gaseous mercury goes to liquid state at 629.88 K .
Step 3. The liquid mercury at 629.88 K is cooled until it reaches 297 K.
This series of steps can be represented through the following diagram:
Hg (g) (650 K) → Hg (g) (629.88 K) → Hg (l) (629.88 K) → Hg (l) (297 K)
(1) (2) (3)
Then the total heat involved in the process will be equal to the sum of the heats inherent to steps 1, 2 and 3. We proceed to calculate the heats for each of the steps.
Step 1:
The heat in step 1 will be given by
Q = n Cp ΔT
where n is the number of moles of mercury, Cp is the heat capacity and ΔT is equal to the difference between the temperatures at the end (T₂) and at the beginning of the process (T₁), that is to say
ΔT = T₂ - T₁
You should know that the heat capacity or thermal capacity is the energy needed to increase the temperature of a certain substance in a unit of temperature. The heat capacity of mercury is Cp = 27.983 J / mol K
Then the heat in step 1 will be,
Q₁ = 75.0 g x
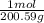x 27.983
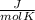x (629.88 K - 650 K)
→ Q₁ = - 210.5 J
Step 2:
In this step a change in the state of the mercury occurs, since it condenses from a gaseous state to a liquid state. In this case the heat involved in the process will be given by ,
Q = - n ΔHvap
where ΔHvap is the enthalpy of vaporization. The enthalpy of vaporization is the amount of energy necessary for the mass unit of a substance that is in equilibrium with its own vapor at a pressure of one atmosphere to pass completely from the liquid state to the gaseous state. Therefore, to determine the energy necessary for the mercury to pass from gaseous state to liquid, the negative of the enthalpy of vaporization must be taken, as it is done in the previous equation with the minus sign that is placed.
The enthalpy of vaporization of mercury is ΔHvap = 59.11 kJ/mol
Then the heat in step 2 will be,
Q₂ = - 75.0 g x
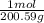x 59.11
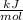
→ Q₂ = 22.10 kJ → Q₂ = 22100 J
Step 3:
The heat in step 3 will be
Q₃ = n Cp ΔT = 75.0 g x
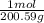x 27.983
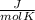x (297 K - 629.88 K)
→ Q₃ = - 3483 J
Finally the heat involved in the overall process will be ,
Q = Q₁ + Q₂ + Q₃ = - 210.5 J - 22100 J - 3483 J = - 25794 J
→ Q = - 25.8 kJ
So, the heat lost when 75.0 g of mercury vapor at 650 K condenses to a liquid at 297 K is - 25.8 K