Answer: AH = 24 unit
Explanation:
Since, in triangles ABC and BHC,
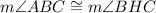 ( Right angles)
( Right angles)
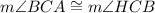 ( Reflexive )
( Reflexive )
Hence, By AA similarity postulate,
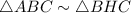
By the property of similar triangle,
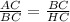
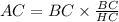
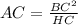
Here, BC = 9 unit and HC = 3 unit,
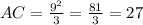
Since, by the below diagram,
AH = AC - HC
AH = 27 - 3
AH = 24 unit