Question

Jamie has 8/10 of a candy bar leftover. He wants to split it into 1/3 pieces. How many whole 1/3 pieces can he make?

Answer 1

Jamie can make 2 complete pieces of 1/3 and one piece corresponding to a portion of 0.4, which in fractional number corresponds to 2/5

Explanation:

Jamie has
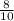`(8)/(10)` of a candy bar, and wants to split it into an unknown number of
`(1)/(3)` pieces.

Then, to get the number of complete pieces of
`(1)/(3)` that can be done, simply divide
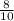`(8)/(10)` (portion of the leftovers of a chocolate bar) by
`(1)/(3)` (pieces in which you want to divide).

`((8)/(10) )/((1)/(3) ) =(8)/(10) *(3)/(1) =(24)/(10) =(12)/(5) =2.4`

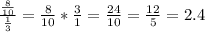
This is not an integer, which can be interpreted as follows: Jamie can make 2 complete pieces of 1/3 and one piece corresponding to a portion of 0.4, which in fractional number corresponds to 2/5. Or, it can easily be said that Jamie can make 2.4 pieces of 1/3.

Another way to get the solution to this problem is as follows:

The number of pieces to be calculated is called "x".

To find out the portion of the candy bar that corresponds to each piece, divide the total portion of the candy bar by the number of pieces x.

Then
`((8)/(10) )/(x) =(1)/(3)`

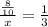
It is desired to isolate the value of x. For that multiply each side by x, obtaining :

`(8)/(10) =(1)/(3) *x`

Then, divide each side by
`(1)/(3)` so that we can have the variable x on one side and its value on another.

`((8)/(10) )/((1)/(3) ) =((1)/(3) *x)/((1)/(3) )`

`((8)/(10) )/((1)/(3) ) =x`

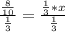
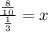
The same operation previously performed is obtained in this way, then the result will be the same.

Answer 2

2

Explanation:

The question is essentially asking "How many one-third pieces are there in eighth-tenths"?

So we can find the answer by dividing
`(8)/(10)` by
`(1)/(3)` and taking the whole number. We show below:

`((8)/(10))/((1)/(3))\\=(8)/(10)*(3)/(1)\\=(24)/(10)\\=2(2)/(5)`

So there can be 2 whole one-third pieces.