Answer:
a. Domain: (-∞, ∞)
Range: (0,∞)
b. Domain: (-∞, ∞)
Range: (0,∞)
c. Domain: (-∞, ∞)
Range: (-∞,0)
d. Domain: (-∞, ∞)
Range: (-∞,0)
e. Domain: (-∞, ∞)
Range: (0,∞)
Explanation:
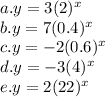
These equations are all exponential functions. Exponential functions are curves which approach a horizontal asymptote usually at y=0 or the x-axis unless a value has been added to it. If it has, the curve shifts. None of these have that and their y - values remain between 0 and ∞. This is the range, the set of y values.
However, the range of exponentials can change based on the leading coefficient. If it is negative the graph flips upside down and its range goes to -∞. C and D have this. Their range is (-∞, 0)
In exponential functions, the x values are usually not affected and all are included in the function. Their domain is (-∞, ∞). All of these equations have this domain.
a. Domain: (-∞, ∞)
Range: (0,∞)
b. Domain: (-∞, ∞)
Range: (0,∞)
c. Domain: (-∞, ∞)
Range: (-∞,0)
d. Domain: (-∞, ∞)
Range: (-∞,0)
e. Domain: (-∞, ∞)
Range: (0,∞)