Question

LOOK AT CHART BEFORE THE BULLET PART:

● Suppose Sal’s total profit on lunch specials for next month is $1596. The profit amounts are the same: $3 for each sandwich and $4 for each wrap. Fill in the empty boxes above with the correct information.
Show your work:

Answer 1

1st blank:
`\text{Slope(m)}=-(3)/(4)`

2nd blank:
`\text{y-intercept}=399`

3rd blank: Slope-intercept form:
`y=-(3)/(4)x+399`

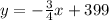
Explanation:

Let x be the number of sandwiches and y be the number of wraps.

We have been given a chart of values, which represents Sal's total profit on lunch specials for two months. We are asked to fill in the empty boxes.

We have been given that Sal gets a profit of $3 after selling each sandwich, so Sal's profit after selling x sandwiches will be 3x.

As each wrap gives a profit of $4, So Sal's profit after selling y wraps will 4y.

Since Sal’s total profit on lunch specials for next month is $1596. We can represent this information in an equation as:

`3x+4y=1596`

We can see that our equation is in standard form, so let us convert it in slope-intercept form of equation.

Since we know that equation of a line in slope-intercept form is:
`y=mx+b`, where,

m = Slope of line,

b = y-intercept or initial value.

Let us subtract 3x from both sides of our equation.

`3x-3x+4y=1596-3x`

`4y=1596-3x`

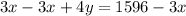
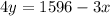
Let us divide both sides of our equation by 4.

`(4y)/(4)=(1596-3x)/(4)`

`y=(1596)/(4)-\fraxc{3x}{4}`

`y=399-(3)/(4)x`

`y=-(3)/(4)x+399`

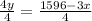
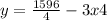
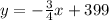
Therefore, equation
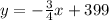`y=-(3)/(4)x+399` represents the Sal's total profit for 2nd month in slope-intercept form of equation.

Upon comparing our equation with slope-intercept form of equation we can see that slope of our line is
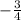`-(3)/(4)` and y-intercept is 399.