Answer: 6 unit
Explanation:
Here, two triangle PQR and JXY are given,
In which QS and XZ are the medians of triangles PQR and JXY respectively,
Also,

Since, the corresponding sides and corresponding median of similar triangles are in same ratio,
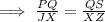
Here, PQ=9 unit , XZ=4 unit, QS=XJ unit,
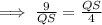
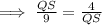
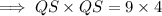
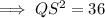
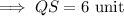
Note : Since, it is the measurement of length, this is why we did not take √36 = - 6.