Question

Suppose (1,19) is on the graph of y = f (x). Which of the following points lies on the graph of the transformed function y = f(1/5x)?

Answer 1

A points that lies on the graph of the transformed function y = f(1/5x) is: A. (5, 19).

In Mathematics and Geometry, a function can be stretched by multiplying it with a numerical value that is either greater than 1 or less than -1.

Based on the information provided, we can logically deduce that the graph of the parent function y = f(x) was horizontally compressed by a positive factor of 1/5, in order to produce the graph of the transformed function.

In this context, we would multiply the x-coordinate of the given point by 5 as follows;

(x, y) → (5x, y)

(1, 19) → (5, 19)

Answer 2

(5,19) lies on the graph of the transformed function y = f(1/5x)

Explanation:

Suppose (1,19) is on the graph of y = f (x)

the graph of the transformed function y = f(1/5x)

`y=f((1)/(5)x)`

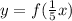
1/5 is multiplied with x in f(x)

1/5 is less than 1 so there will be a horizontal stretch in the graph by the factor of 1/5

To make horizontal stretch we change the point

f(x)=f(bx) then (x,y) --->( x/b,y)

We divide the x coordinate by the fraction 1/5

(1,19) ---->
`((1)/((1)/(5)) , 19)= (5,19)`

So (5,19) lies on the graph of the transformed function y = f(1/5x)