For this case, we perform the conversions:
First roll:
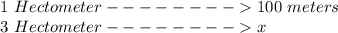
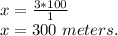
We make a rule of three to determine the number of "c" boxes that can be packed with 300 meters of adhesive tape.
1 -----------> 4.2
c -----------> 300
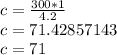
You can pack 71 boxes.
Second roll:

We make a rule of three to determine the number of "c" boxes that can be packed with 70 meters of adhesive tape.
1 -----------> 4.2
c -----------> 70
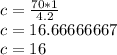
You can pack 16 boxes.
Third roll:
1 -----------> 4.2
c -----------> 50
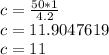
You can pack 11 boxes.
Thus, in total you can pack
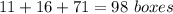
Answer:
98 boxes