Answer:
Option B. is the right answer.
Explanation:
We have to simplify the given fraction
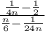
Now we will solve numerator first
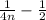
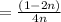
Then we will solve denominator

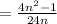
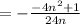

Now we put numerator and denominator in the form of a fraction.

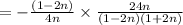
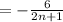
Therefore option B is the right answer.