Answer:
A is correct
Explanation:
The base of a solid in the region bounded by the two parabolas
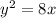 and
and
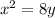 .
.
Two parabola equation:
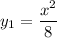
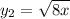
Cross sections of the solid perpendicular to the x-axis are semicircles.
Diameter of semicircle
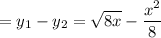
Radius of semicircle (r)

Thickness of solid
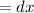
Range of

Volume of solid = Area of semicircle x Thickness
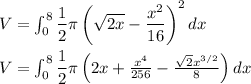
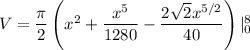
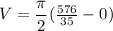
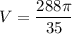
Hence, A is correct