Question

Please help me with this!!!!

Answer 1

`\large\text{Slope AB}\ =-(3)/(2)}`

`\large\text{R(4, -7)}`

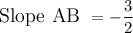
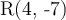
Explanation:

The formula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

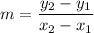
We have the points A(-6, 8) and B(-2, 2). Substitute:

`m=(2-8)/(-2-(-6))=(-6)/(-2+6)=(-6)/(4)=-(3)/(2)`

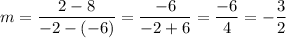
The hypotenuse of triangle QRS is on the same line as the hypotenuse of triangle ABC. Therefore the line QR has the same slope as the line AB.

We have Q(2, -4) and R(x, y). Substitute to the formula of a slope:

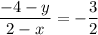`(-4-y)/(2-x)=-(3)/(2)` cross multiply

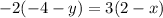`-2(-4-y)=3(2-x)` use distributive property

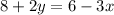`8+2y=6-3x` subreac 8 from both sides

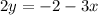`2y=-2-3x` divide both sides by 2

`y=-(3)/(2)x-1\qquad\boxed{(*)}`

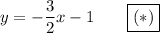
The hypotenuse of triangle QRS is one-half the length of AB.

The formula of a distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

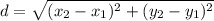
Calculate the distance between A and B:

`|AB|=√((-2-(-6))^2+(2-8)^2)=√(4^2+(-6)^2)=√(16+36)=√(52)\\\\=√(4\cdot13)=\sqrt4\cdot√(13)=2√(13)`

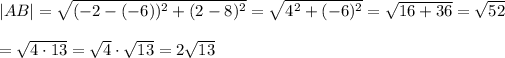
Therefore

`|RQ|=(2√(13))/(2)=√(13)`

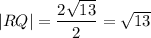
Substitute coordinates of the point R(x, y) and Q(2, -4) to the formula of a distance between two points:

`√((2-x)^2+(-4-y)^2)=√(13)\to(2-x)^2+(-4-y)^2=13\qquad\boxed{(**)}`

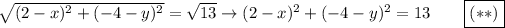
Substitute
`\boxed{(*)}` to
`\boxed{(**)}`:

`(2-x)^2+\left[-4-\left(-(3)/(2)x-1\right)\right]^2=13\\\\(2-x)^2+\left(-4+(3)/(2)x+1\right)^2=13\\\\(2-x)^2+\left((3)/(2)x-3\right)^2=13\qquad\text{use}\ (a-b)^2=a^2-2ab+b^2\\\\2^2-2(2)(x)+x^2+\left((3)/(2)x\right)^2-2\left((3)/(2)x\right)(3)+3^2=13\\\\4-4x+x^2+(9)/(4)x^2-9x+9=13\qquad\text{combine like terms}\\\\\left((4)/(4)x^2+(9)/(4){x^2}\right)+(-4x-9x)+(4+9)=13\\\\(13)/(4)x^2-13x+13=13\qquad\text{subtract 13 from both sides}`

`(13)/(4)x^2-13x+13=13\qquad\text{subtract 13 from both sides}\\\\(13)/(4)x^2-13x=0\qquad\text{divide both sides by 13}\\\\(1)/(4)x^2-x=0\\\\x\left((1)/(4)x-1\right)=0\iff x=0\ \vee\ (1)/(4)x-1=0\\\\(1)/(4)x-1=0\qquad\text{add 1 to both sides}\\\\(1)/(4)x=1\qquad\text{multiply both sides by 4}\\\\x=4\\\\\boxed{x=0\ \vee\ x=4}`

Put the values of x to
`\boxed{(*)}`

`x=0\\\\y=-(3)/(2)(0)-1=0-1=-1\to(0,\ -1)\\\\x=4\\\\y=-(3)/(2)(4)-1=-3(2)-1=-6-1=-7\to(4,\ -7)`

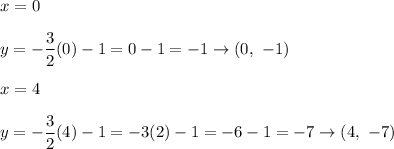
As the triangle ABC and the QRS triangle are similar, then AB corresponds to QR not RQ. Thus, the coordinates of the R point are (4, -7).

Look at the picture.

Answer 2

Slope AB = -3/2

R = (4, -7)

Explanation:

AB (-6 , 8) and (-2 , 2)

Slope AB = (8 - 2) /(-6 + 2) = 6/-4 = -3/2

Triangle QRS , QR is half of AB, same orientation and given Q (2 , -4) so R = (4, -7)